There is an effort going on to improve the double bond assignment machinery in the CDK, which is great. Of interest to me, however, is how many possible arrangements of double bonds can you have in fused ring systems. This was mentioned in at least one previous post - or perhaps two.
However, lets get a very rough upper bound; how many ways are there to color the N edges of a graph with two colors? This is 2 to the power N, or the set of all subsets of the edges. Of course, many of these are chemically meaningless, where atoms have too high a valence. So filter out those where adjacent edges have the same color - or more exactly, where adjacent edges are colored with the 'double bond' color (let's call it '2').
The image shows a sketch of the simple procedure (above) and a slightly better approach (below). The better way of doing things is similar to the k-independent chessboard solution (sorry to link to my own pages so much - but it is relevant!). The idea is to use the symmetries of the graph (or chessboard) to prune solutions that must have already been tried.
This does seem to work, but there are a huge number of solutions - even for relatively small graphs. For example, fusanes with just 4 rings have thousands of partial solutions. For these four examples, there is quite a variation:
The most symmetric (green) example has the least - of course - but the large numbers of solutions of size 5 for the orange example is odd. It's a bit difficult to look through these to see why, unfortunately. What is much easier is the 'full' solutions of size 9. For example, for the green graph:
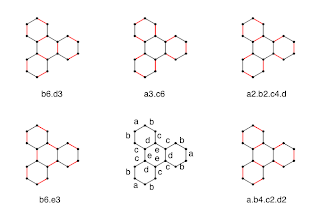
A bit difficult to distinguish these drawings - actual double lines are clearer, it seems. Anyway, below each is a kind of 'name' based on the bond equivalence classes (a-e) in the lower center. So, "b3.d3" means three 'b' bonds and three 'd' bonds are colored.
However, lets get a very rough upper bound; how many ways are there to color the N edges of a graph with two colors? This is 2 to the power N, or the set of all subsets of the edges. Of course, many of these are chemically meaningless, where atoms have too high a valence. So filter out those where adjacent edges have the same color - or more exactly, where adjacent edges are colored with the 'double bond' color (let's call it '2').
The image shows a sketch of the simple procedure (above) and a slightly better approach (below). The better way of doing things is similar to the k-independent chessboard solution (sorry to link to my own pages so much - but it is relevant!). The idea is to use the symmetries of the graph (or chessboard) to prune solutions that must have already been tried.
This does seem to work, but there are a huge number of solutions - even for relatively small graphs. For example, fusanes with just 4 rings have thousands of partial solutions. For these four examples, there is quite a variation:
A bit difficult to distinguish these drawings - actual double lines are clearer, it seems. Anyway, below each is a kind of 'name' based on the bond equivalence classes (a-e) in the lower center. So, "b3.d3" means three 'b' bonds and three 'd' bonds are colored.
Comments