There is an interesting book by W. T. Tutte called 'Graph Theory as I have known it' which is a cross between a normal mathematical text and a biography. So it's a description of the areas he was interested in, and his theorems. One thing that interested me was the use of a 'twist' operation on cubic graphs like so:
Where for the edge between vertices x and y labelled 'A' we reconnect the surrounding edges to form the arrangement on the right hand side. So detach edge D from y and connect it to x, and vice versa with edge C. The lower part of the picture shows what happens for a loop-edge - it transforms to a multi-edge.
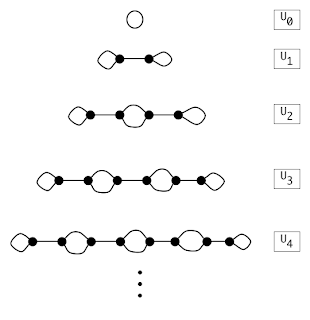
This operation is used on a family of 'base' graphs looking like this:
with the first in the list is a vertexless loop graph - that is, it has no vertices and a single edge. From these base graphs, the twist operation can form any cubic graph. Note that all of Un are cubic with 2n vertices.
For example, from U3 we can get to both of the (simple) graphs with 6 vertices by the following sequence:
In this diagram, the twist is being applied to the red edge, then the blue, then the green, etc. The final step converts the prism (G6) to K3,3 (G7) while the other steps involve non-simple graphs with loops and multiple edges.
One of Tutte's uses for these transformations was to show that the number of 1-factors (perfect matching) J of a graph can be calculated by J(G) + J(GA) = J(H) + J(HA) where GA is a graph with the edge A deleted. So, starting with a base graph U - which has J = 1 except for U0 where J = 2. Then use that value to determine the number of 1-factors in the next graph in the sequence, and so on.
It does make me wonder if there is a way to generate cubic graphs from these base examples, by these twists. From a few simple examples it is clear that there would be a lot of redundancy at the leaves of the generated tree, but possibly that could be handled with canonical path augmentation in some way.
Where for the edge between vertices x and y labelled 'A' we reconnect the surrounding edges to form the arrangement on the right hand side. So detach edge D from y and connect it to x, and vice versa with edge C. The lower part of the picture shows what happens for a loop-edge - it transforms to a multi-edge.
This operation is used on a family of 'base' graphs looking like this:
For example, from U3 we can get to both of the (simple) graphs with 6 vertices by the following sequence:
In this diagram, the twist is being applied to the red edge, then the blue, then the green, etc. The final step converts the prism (G6) to K3,3 (G7) while the other steps involve non-simple graphs with loops and multiple edges.
One of Tutte's uses for these transformations was to show that the number of 1-factors (perfect matching) J of a graph can be calculated by J(G) + J(GA) = J(H) + J(HA) where GA is a graph with the edge A deleted. So, starting with a base graph U - which has J = 1 except for U0 where J = 2. Then use that value to determine the number of 1-factors in the next graph in the sequence, and so on.
It does make me wonder if there is a way to generate cubic graphs from these base examples, by these twists. From a few simple examples it is clear that there would be a lot of redundancy at the leaves of the generated tree, but possibly that could be handled with canonical path augmentation in some way.
Comments